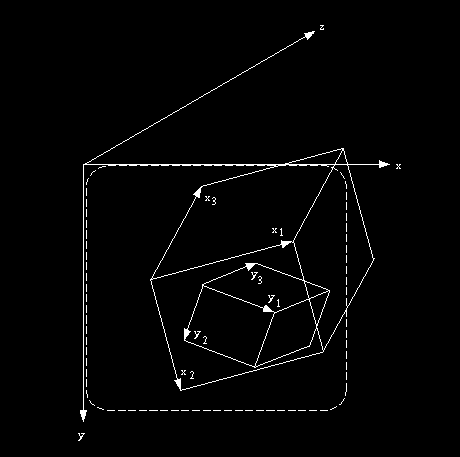
Fig 3.1: Illustration of scene, structure, view space coordinate systems.
Voxel: A cuboid elemental volume, three-dimensional (3D) analog of a pixel, abbreviation for volume element.
Cell: An elemental region of an n-dimensional (nD) space, nD analog of a pixel.
Grey Picture, Pixel Intensity, Pixel Size: A grey picture is a rectangular (two-dimensional (2D)) array of pixels in which each pixel has a number called pixel intensity (or density) associated with it. Pixel size is the length of each side of the rectangle, usually expressed in mm.
True-Color Picture: A rectangular 2D array of pixels in which each pixel has three intensity values associated with it, one for each of the red, green, and blue components of color.
Pseudo-Color Picture: A grey picture together with a table that associates for each pixel intensity value a triple of numbers indicating the red, green and blue component values of a color.
We use the term picture to refer to any of grey, true-color, and pseudo-color pictures and pixel intensity to refer to the value(s) associated with a pixel.
Binary Picture: A grey picture in which every pixel has only one of two intensities, 0 and 1, associated with it.
3D Scene, Voxel Intensity, Slice, Slice Spacing, Voxel Size : A 3D scene is a rectangular (3D) array of voxels in which each voxel has a number called voxel intensity (or density) associated with it. A stack of parallel cross-sectional images of a body region obtained via computerized tomography (CT) or magnetic resonance (MR) imaging constitutes a 3D scene. A slice of a 3D scene is a layer of voxels corresponding to a cross-sectional image together with the associated voxel intensities. We assume that the voxels in a slice extend up to half the distance from the cross-sectional plane of the slice to the adjoining cross-sectional planes on the two sides. Thus, in a stack of equispaced cross-sectional images the cross section of the voxels equals the pixels and the height (or thickness) of the voxels equals the spacing between cross-sectional planes, called slice spacing. A voxel size of abc means that the voxel cross section has dimension ab (usually, a=b) and its height is c. The unit of measurement is usually mm. However 3DVIEWNIX handles a variety of other units. The data generating device and the mechanism of transporting data into 3DVIEWNIX should ensure that information about the unit of measurement is properly recorded.
nD Scene, Cell Intensity, Slice, Cell Size : An nD scene is a rectangular (nD) array of cells in which each cell has a number called cell intensity (or density) associated with it. For example, a set of stacks of parallel cross-sectional images of a body region containing a dynamic object, such as a beating heart or a moving joint, constitutes a 4D scene. Each stack in the set represents the 3D body region at a particular time instant at which the dynamics may be thought of as being frozen. A 4D scene can thus be thought of as a set of related 3D scenes. A slice of a 4D scene is simply a slice of a constituent 3D scene. (Higher-dimensional (greater than 4D) scenes are not common in biomedical imaging. However, such scenes can be created for image processing purposes. For example, it may be useful to express a 4D scene as a surface in a 5D space, where the fifth dimension, representing the height of the surface, is taken to be the cell intensity. Given such a surface, it is useful in certain operations to obtain a "distance map" of the surface as a 5D scene in which the cell intensity represents the shortest distance to the surface from the cell.) The size of the cells is defined as in the case of the voxels. A cell size of abcd for the 4D case means that the 2D cross section of the cell (i.e., pixel size) is of dimension ab (usually a=b). The size of the cell in the third dimension equals c and the size in the fourth dimension equals d. The unit of measurement in the first three dimensions is usually mm and that in the fourth dimension is usually msec (for time). 3DVIEWNIX allows these units to be different in different dimensions, but such information has to be properly recorded while porting data into 3DVIEWNIX.
Many operations in 3DVIEWNIX allow treating an nD scene as a single entity. This brings convenience to the user and often makes certain operations possible which otherwise would not be possible.
The notion of an nD scene subsumes the notion of a picture and of a 3D (and 4D) scene. Therefore, we often use the term scene in this general sense to refer to any nD scene or to a picture.
Binary Scene: A scene with only two possible cell intensity values, 0 or 1. Cells with intensity 1 are called 1-cells and those with intensity 0 are called 0-cells. Note that the notion of a scene subsumes the notion of a binary scene.
Scene Domain: The set of all pixels/voxels/cells within a scene.
Cell Coordinates, Slice Indexes, Scene Coordinate System: The locations of a cell within a scene domain are expressed in terms of the number of the cell in each dimension, known as the cell coordinate in that dimension. The coordinates of a cell located at the 10th column, 5th row, 20th slice, and 7th time instance of a dynamic 4D scene are (10, 5, 20, 7). We refer to these as the x_1, x_2, x_3 and x_4 coordinates of the cell, respectively. In a 3D scene, all cells within a given slice have a fixed x_3 coordinate. In a 4D scene, all cells within a given slice have a fixed x_3 and a fixed x_4 coordinate. These fixed coordinates are called the indexes of the slice. In a 3D scene, therefore each slice has one index and in a 4D scene each slice has two indexes. This coordinate system used for determining the location of cells is called a scene coordinate system. We assume it to be right handed. This means that, for the 3D case, if you stretch out the thumb, forefinger and middle-finger of your right hand such that they are roughly mutually perpendicular, then you can turn your hand so that these fingers point in the x_1, x_2, x_3 directions, respectively (see Figure 3.1).
Region-of-Interest (ROI): Most generally, ROI refers to a region (subset) of the scene domain. There are no restrictions on the shape of this region. For example, an ROI may be the set of pixels enclosed within an arbitrary closed curve drawn with a mouse by the user on a picture. Or it may be a set of voxels in a 3D scene specified by the user by drawing a closed curve in each of a set of slices of the scene. The term is often used to refer to a rectangular region of the scene domain. For example, it may be the set of voxels enclosed within a rectangular box indicated by the user.
Gradient, Gradient Direction, Gradient Magnitude : The gradient of a scene at a cell is a vector quantity. Its direction indicates the direction in which cell intensity changes most rapidly in the vicinity of the cell in question. Its magnitude is the rate of change of intensity in this direction. Several methods are available to compute these entities.
Feature: It is a term used to refer to any attribute or characteristic of an object . A feature may be derived from a scene that has captured information about the object. For example, we may simultaneously capture two 3D scenes for a human head via MR imaging, one constituting predominantly the so-called T1 property and the other proton density . Every voxel now has two features -- T1 value and proton density. (For this to make sense the two scene domains should correspond to exactly the same region of the head.) It is also possible to obtain derived features as opposed to those that are measured or imaged as in the previous example. Gradient magnitude at every voxel in a given scene, for example, constitutes a derived feature. Features are used mainly for identifying objects in given scenes.
ROI Statistics: Minimum, maximum, mean, and standard deviation of the values of certain features such as voxel density and gradient magnitude within a specified ROI. These entities are useful in understanding how the feature values are distributed within a given region of an object.
Histogram of Features: It is a graph of the cell feature values in a scene versus the number of cells in the scene that have each feature value. The notion of the histogram obviously applies to any ROI also. Often it is of interest to plot the histogram only for a given slice or for an ROI within the slice.
Object, Structure, Shell: Certain entities about which information is captured in scenes are called objects. These constitute meaningful forms and shapes within a scene domain which a user can roughly delineate on a display of the slices of the scene. The notion of an object is more general than the usual and common meaning conveyed by this word. An object may be a static object, such as a human skull, about which information is captured in a 3D scene that is obtained via CT (see for various medical imaging modalities). It may be a beating heart derived from a 4D scene obtained via MRI. It may be an isoactivity surface derived from a 3D scene representing a Positron Emission Tomographic (PET) scene of a human brain. It may be an isodose surface of a radiation treatment plan (see Chapter 12 in ) for a particular region of the body. It may also constitute a computer model of a particular prosthetic device (see Chapter 13 in .)
A structure is a particular representation of a particular aspect of an object in the computer. In the heart example above, the object, called heart, may be represented by a set of structures, say a set of 3D surface representations (derived from each 3D subscene of the 4D MR scene), each 3D surface constituting the form and shape of the heart at a particular time instant in the heart cycle. If the 4D scene is created by acquiring data for each of 8 time instants, and if we derive a surface representation from each time instant, we have the object heart represented by 8 structures. We may identify multiple objects, say the heart muscle and the blood pool, in the scene data. In this case we have two objects each represented by 8 structures.
Several forms of structures are used in 3DVIEWNIX. The main forms are covered under a generic term called shell . A shell is simply a collection of structure elements together with a set of property values associated with each structure element, such as opacity, surface normal (see below), etc. Two types of structure elements are considered at present -- voxels and voxel faces. The structures using these as structure elements are called Shell0 and Shell1, respectively. In shell representation, the structure elements may cover just the boundary, or some region in the vicinity of the alleged boundary of the object. The first case is very specialized. In this case the shell is very thin; it has a thickness of one structure element and all structure elements have a fixed opacity value (usually 100%) assigned to them. We call such shells binary shells. The second case is very general and subsumes the first case. The structure elements in this case may cover the entire region occupied by the object. Since the opacity value assigned in this case can be any value between 0% to 100%, we call such shells non-binary shells. Non-binary shells allow retaining fuzziness inherent in object definition, whereas, in binary shells, the decision as to where the object lies is binary. Note that binary shells essentially give a surface representation of an object and non-binary shells provide a volume representation.
Structure Coordinate System: Every structure has a right-handed structure coordinate system associated with it. The coordinates of the structure elements are expressed relative to this coordinate system. We use y_1, y_2, y_3 to represent these coordinates.
Structure System, Parameter Vector : A structure system is simply a collection of related structures along with a specification of the role of each structure in the collection. This is a powerful central notion within 3DVIEWNIX. It facilitates visualization, manipulation, and analysis of an object assembly in an integrated and comprehensive fashion. The structures in the structure system may come from the same imaging modality or from different modalities (such as brain information from MRI and PET) or from simulation or computational procedures (such as isodose surfaces in radiation treatment planning). They may come from different time instances in a longitudinal study. They may pertain to different subjects (here the objective may be comparing the form/shape/function of the same object in different subjects). They may represent a rigid, non-rigid, static or a dynamic object. Any combinations of the above factors are also possible. As an example, consider a structure system consisting of 14 structures, three of them constituting the three time instances of one dynamic object, (say, heart muscle), derived from one modality (say, MRI), another three structures constituting the three time instances of the same dynamic object obtained from another modality (say, PET), another six structures constituting three time instances for each of the two modalities of another dynamic object (say, the blood pool in the heart chambers), the 13th structure representing a static object (say a diseased liver derived from MR), and the 14th structure representing an isodose surface computed for planning radiation treatment of the static object.
Parameter Vector is a mechanism of indicating the role of each structure in the structure system. In the above example, we have three parameters to consider: object number (out of 4), time instant (out of 3), and modality (out of 2). If we use a 3-tuple with the first element indicating object number, the second indicating time instant, and the third indicating modality, we may associate a 3-tuple called a parameter vector with each of the 14 structures. The 3-tuple (1, 3, 2) then means that the structure to which it is assigned is: object #1 (heart muscle), time instant 3, and modality 2 (PET). We may assign time instants 4 and 5 to the 13th and 14th structures, respectively (if none of the three instants associated with the dynamic structures is relevant) and assign object # 3 and 4 to them and modality 1 (MR) and 3 (to indicate that it is different from MR and PET). The fourteen parameter vectors associated with this structure system are: (1, 1, 1), (1, 1, 2), (1, 2, 1), (1, 2, 2), (1, 3, 1), (1, 3, 2), (2, 1, 1), (2, 1, 2), (2, 2, 1), (2, 2, 2), (2, 3, 1), (2, 3, 2), (3, 4, 1), (4, 5, 3).
It is important to note that the structures in the structure system should be properly "registered" to carry out meaningful operations on them. The parameter vectors come in handy in applying visualization, manipulation, and analysis operations on structure systems.
Structure Plan : It represents a collection of structures together with information about geometric transformations (translation, rotation and scaling) associated with each structure in the set. Structures themselves are not stored in the structure plan but information as to where they can be found is stored. The geometric transformations indicate the correct relationship between the constituent structures in the structure plan.
As an example, suppose we acquire two scenes via CT and MRI of the head of a patient. We are interested in extracting several structures from each scene and in representing them all in a single assembly with correct geometric relationship. We may use the skin surface to "register" the two data sets, that is to find out the geometric transformation that we need to apply on the set of structures obtained from one scene so that they are in the correct geometric relationship with the structures obtained from the other scene. The geometric transformation to be applied to each structure can be expressed relative to some fixed coordinate system, say a coordinate system fixed to the CT scanner. The individual structures should be stored in the same file. The result of this process of registration is essentially a structure plan.
Like a structure system, the notion of a structure plan has more general applicability than that indicated above. A structure plan may be the result of a surgical simulation in which structures are moved relative to other structures in the assembly. The final position and orientation information is then captured in the structure plan. A structure plan may be the result of analysis of the motion of a set of rigid objects such as the bones at a joint. Consider a joint with 4 component bones for each of which 8 different positions have been obtained via imaging to capture one particular motion sequence of the joint. The motion of the joint can be represented by a structure plan that consists of 32 structures. Each of the 4 groups of 8 structures represents different positions of the same object. Hence the structures in a given group all point to a single structure. The associated geometric transformations indicate the motion of the joint.
Surface Normal : It is an entity (a unit vector) assigned to every structure element that indicates the direction that is perpendicular to the "surface" of the object represented by the structure. It is needed for creating a shaded 3D display of the structure. This is mainly because the properties of reflection of light from a structure are governed by the surface normal at various elements of the structure.
Rendition: A picture representing a photograph-like depiction of a structure generated by a computer algorithm.
Display Data, Display Data Dimension, Picture Indexes : Any collection of pictures all having the same size represent display data. The pictures may or may not have any relationship. For example, some of the pictures in the collection may be the result of the grey map operation (see next section) on a set of slices of a scene. Others may be renditions of a structure system derived from the scene, some of which are surface renditions and the rest volume renditions.
Each display data set has a dimensionality associated with it. If the pictures in the set have no relationship, the dimensionality is 3. The third dimension indicates the number of pictures in the set. It is possible to create display data with dimensionality greater than 3. Consider a set of renditions of a dynamic structure created for each of 8 time instants for each of which 60 pictures are generated by rotating the time frozen structure about some fixed axis at 6 increments. The display data now consists of 480 pictures and have a dimensionality of 4. The first two dimensions correspond to the columns and rows of the pictures, and the third and fourth correspond to time and viewing angle, respectively. Every picture in the data set can be indexed by two numbers in this example, the time instant and the view number. These are called the indexes of the picture. Display data of dimensionality greater than 4 are also possible.
View Space, View Space Coordinate System : View space is the 3D space in which object displays are created. A display may show simply a slice of a scene or a rendition of a structure. We associate a right-handed coordinate system (x, y, z) with the view space. We think of the xy-plane of this space to be the display screen, with the origin situated at the upper-left corner of the screen, the x-axis going from left to right, the y-axis going from top to bottom, and the z-axis going into the screen. Figure 3.1 illustrates the relationship between the coordinate systems associated with scene, structure and the view space. When a slice of a scene is displayed (without any rotation), the x_1 and x_2 coordinates of its cells increase in the x and y directions, respectively, of the view space.

Fig 3.1: Illustration of scene, structure, view space coordinate systems.
3.2 Operation-Related
Preprocessing: Any operation that is used toward defining and extracting
structural information that is to be visualized, manipulated and
analyzed from input scene or structure data.
Visualization: Any operation that is used toward being able to see structural information from input scene, structure, or display data.
Manipulation: Any operation that is used for altering a structure or the relationship of structures in a structure system.
Analysis: Any operation that extracts quantitative information about the structures being studied from input scene or structure data.
3D Imaging: Any operation related to preprocessing, visualization, manipulation, and analysis.
The above categories of operations are not strictly mutually exclusive as we already pointed out. But they provide a systematic scheme for dealing with the imaging operations that are commonly used. More importantly, they form the basis of the menu system used in 3DVIEWNIX that provides the user with various commands and options to realize imaging operations.
Process: When used in a technical sense, it refers to an independent program that carries out an operation.
Volume-of-Interest (VOI) : It is an operation that converts a Scene A into another Scene B. The domain of Scene B is a rectangular ROI specified for Scene A on a slice display. The extent of the ROI in the 3rd, 4th and higher dimensions is specified by indicating the limits in those directions. For example, for a 4D scene of a dynamic object, in addition to a rectangular ROI on a slice display, the number of the first and the last slice and the first and last time instance in Scene A to be included in Scene B are also specified. Effectively, a subset of the domain of Scene A becomes the domain of Scene B.
The range of cell intensity values for Scene B is specified also as a subset of the range of cell intensity values of Scene A. For example, cell intensities in Scene A may range from 0 to 1000 and for Scene B we may choose the range to be 100 to 200. All intensities in Scene A that are less than or equal to 100 and greater than or equal to 200 are set to 0 and 100 in Scene B, respectively. All intensities between 100 and 200 in Scene A are set to values between 0 and 100 in Scene B proportionately.
The main objective of this operation is to reduce the amount of data that is to be handled in subsequent operations. This is done by reducing the number of cells and the number of intensity values that need to be stored.
Interpolation (, Chapter 1): It is an operation that converts a Scene A into another Scene B in which the size of the cells is different from the size of the cells of Scene A. The region of the nD space occupied by the cells of Scene B is more or less the same as the region occupied by the cells of Scene A. As an example, consider a 4D scene with a scene domain of 1001003010 and cell size of 1 mm1mm3mm1msec. The region of the 4D space covered by the scene domain is roughly 100mm100mm90mm100msec. Suppose we wish to create a "higher-resolution" scene with cell size 0.5mm0.5mm0.5mm0.5msec. Interpolation achieves this by subdividing the region of the 4D space into smaller cells and by estimating their intensity values based on the cell intensities of the given scene. The interpolated scene will have a domain roughly of 20020018020.
Intensity Interpolation : It is a class of interpolation methods that estimate cell intensities in Scene B based on cell intensities in Scene A. To estimate a particular cell intensity in Scene B, intensities of cells in Scene A in the neighborhood of the particular cell are considered. The size of the neighborhood depends on the "order" of the interpolating function. For linear interpolation only the immediate neighbors are considered and for higher order interpolation neighbors next to these are also considered. The latter result in smoother intensity distribution in the interpolated scene although they take more computational time than the former.
Distance Transform : It is an operation that converts a binary Scene A into a Scene B with identical scene domain. The intensity of each cell in Scene B represents the shortest distance of the corresponding cell in Scene A from the boundary between 1-cells (cells with intensity 1) and 0-cells (cells with intensity 0) in Scene A. The distance assigned to the cell is negative if the corresponding cell in Scene A is a 0-cell and is positive otherwise. There are several possible interpretations for "shortest distance from boundary". This may be the distance from the boundary within the slice that contains the cell under question, or it may be the distance from any higher-dimensional boundary.
Shape-Based Interpolation : It is a special method of interpolation for binary scenes. The method first converts the given binary Scene A into a non-binary (grey) Scene A^\prime by applying a distance transform to A. Scene A is then converted to Scene B^\prime by applying an intensity interpolation method to A^\prime. Finally Scene B^\prime is converted to a binary Scene B by setting intensity of those cells in B to 1 that have a positive intensity value in B^\prime and of the rest of the cells in B to 0.
Filtering (, Chapter 1): It is an operation that converts a Scene A into another Scene B with identical scene domain. Two types of filtering operations are commonly used -- smoothing and enhancing. In smoothing, sharp intensity changes in Scene A are suppressed in Scene B. In enhancing, intensity changes in Scene A are enhanced in Scene B. If we assign an intensity to each cell v in Scene B that is an average of the intensities of cells that are in the neighborhood of a cell corresponding to v in Scene A, that constitutes a smoothing filtering. If we assign to v the gradient magnitude at the corresponding cell in Scene A, that constitutes an enhancing filtering.
Segmentation: An operation that converts a given Scene A into either a binary Scene B with identical scene domain or a structure -- a binary shell -- that constitutes an object of interest.
Thresholding: A segmentation operation that assigns a value 1 to a cell in Scene B if the corresponding cell in Scene A has an intensity that falls within a specified intensity interval and that assigns a value 0 to the cell otherwise. A less general thresholding operation is one in which a single intensity value is specified. If a cell's intensity in Scene A is above this value, it is assigned a value 1 in Scene B, and a value 0, otherwise.
Surface Detection, Isosurface (, Chapter 1, ): Surface detection is an operation that given a scene outputs a connected surface as a binary shell. If the input is a binary scene, the shell constitutes a connected interface between 1-cells and 0-cells. Connectedness means that within the output shell it is possible to reach any shell element from any shell element without leaving the shell. If the input is a (grey) scene, the interface between the interior and exterior of the structure is usually difficult to determine. Thresholding can be used (if it is effective) to determine this interface, in which case the shell constitutes essentially a connected interface between cells that satisfy the threshold criterion and cells that do not. In the particular thresholding operation specified by a single intensity value, the resulting surface is called an isosurface.
Live-Wire Tracing : A method of automatically finding object boundaries between points specified in a slice. In this method, the first point is specified by the user and the second point is assumed to be the point indicated by the current position of the cursor. The "best" boundary segment between these two points is found automatically based on a set of feature values. If this boundary segment is displayed in real time on a display of the slice, the users get a feeling for the appropriateness of this segment. They can move the cursor and the "live-wire" changes in real-time, snapping on to the alleged boundary if the cursor comes close to the boundary. With a few such segments, usually an entire boundary can be segmented. The result of this operation is a binary scene.
Clustering, Scatter Plot : Given a set of scenes, clustering produces a binary scene or a binary shell. Each input scene constitutes a feature that is to be used in identifying the object of interest. The object is identified by plotting the feature values in a "feature space" and identifying clusters in this space that may correspond to meaningful objects. As an example, suppose we are given two 3D scenes, with identical domains of the same region of the body of a patient corresponding to two MR properties (say, T1 value and proton density). These properties constitute our features, and the feature space is the 2D plane (the features form the abscissa and the ordinate). Every voxel in the common scene domain has two feature values which are plotted as a point in this space. When all voxels are plotted in this fashion to create a scatter plot, we may expect clusters of points to be formed corresponding to different objects (or types of tissue) in the imaged body region, if the features have really discriminating ability. Then we can identify an object by drawing a closed curve on this plot that adequately encloses a corresponding cluster. To create an output binary scene, we need to identify those voxels whose feature values are plotted as a point inside this curve. These are 1-voxels in the binary scene. All the rest are 0-voxels. Derived features, such as the gradient magnitude, can also be used to create scatter plot and to do clustering.
Masking, Interactive Segmentation : Given a Scene A, masking produces another Scene B of identical domain. The intensity of any cell in Scene B is the same as that of the corresponding cell in Scene A if the cell falls within a region specified by the user. If the cell is outside this region, its intensity is set to a constant value that is outside the range of intensities of Scene A. Sometimes the cells falling within the region are assigned the value 1 and those outside are assigned the value 0. This special masking operation is called interactive segmentation.
Classification : It is a process of converting a given set of scenes into a scene, all with identical domains, or into a non-binary shell. If the output is a scene, its cell intensity represents fuzziness or membership value of the cell in the object of interest. In the case of a non-binary shell, the fuzziness or membership value is retained as one of the property values associated with the shell elements.
Grey Scale: Every display device has a grey scale associated with it which consists of a sequence of numbers called grey values each of which represents a certain brightness value on the monitor. The lowest value on this scale represents the dimmest light intensity and the highest value represents the brightest intensity.
Grey Map, Map Level, Map Width: Grey map is an operation that converts a grey picture A into another grey picture B with identical domain. The pixel intensities for picture B are determined by the grey scale of the display device, say, that goes from MIN to MAX, and a range of pixel intensities. This range is specified by two numbers, map level and map width; the range then goes from min = (map level -- (map width/2)) to max = (map level + (map width/2)). If a pixel in picture A has an intensity value less than min or greater than max, it is assigned respectively the value MIN or MAX of the grey scale in picture B. Pixels with intensity lying between min and max are assigned a value between MIN and MAX in a proportionate fashion.
Visual Class : Display devices are grouped into a number of classes called visual classes depending on their ability to display various types of pictures. In 3DVIEWNIX, we consider three visual classes: grey-scale, pseudo-color and direct-color. A display device of the grey-scale visual class can display only grey pictures. Devices of the pseudo-color and direct-color visual class can display, in addition, pseudo-color and true-color pictures. Pseudo-color devices are not as versatile as those of the direct-color visual class. Some color information may be lost when true-color pictures are displayed on a pseudo-color device.
Overlay : It is a mechanism that allows displaying a set of pixels with a fixed intensity value/color overlaid on the display of a picture so that the display of the set of pixels can be turned on or off independently of the display of the underlying picture. This mechanism allows displaying special graphics, such as line drawings and binary pictures, over the display of pictures.
Color Map : When pseudo-color and true-color pictures are to be displayed on pseudo-color and direct-color devices, the color values of the pixels in the given picture has to be properly "mapped" into a color value that is available in the display device. Color map is a table that lists this association.
Reslicing : Given a scene and a set of parallel planes, this operation produces a set of slices depicting intensity distribution along the specified planes. The result can be therefore thought of as another scene.
Cine Display: It is a display of a sequence of related pictures in a rapid succession. The pictures may be the renditions of a structure depicting the different views of the structure as it is being rotated. They may be the successive slices of a 3D scene in which case the display gives the effect of navigating through the scene. The pictures may have a "multidimensional" relationship among them. For example, a set of pictures depicting the different time instances and the different views of a beating heart (as it is being rotated about a fixed axis) at different opacity settings (to make some of the components fade away) has three independent parameters, which can be controlled independently during the display.
Surface Rendering : An operation that creates a rendition of a structure based on a representation of the structure that allows non-fuzzy (or binary) membership values for structure elements. These operations convert any given binary shell into a rendition.
Volume Rendering : An operation that creates a rendition of a structure based on a representation of the structure that allows fuzzy (non-binary) membership values for structure elements. These operations convert any given non-binary shell into a rendition.
We use the term rendering to refer to surface or volume rendering operations.
Diffuse and Specular Reflection , Chapter 1, : These constitute reflective properties of structures under illumination. In diffuse reflection, light incident on a structure element is reflected equally in all directions. In specular reflection, light incident on a structure element is reflected entirely in one particular direction. The former indicates matteness of the structure and the latter its mirror-like behavior or shininess. In practice, structures are neither purely matte nor act purely as a mirror, but have a combination of these properties. Surface normal information is needed for calculating the components of reflected light that reach the viewpoint because of both these reflective properties.
Transmission : When the opacity assigned to a structure element is less than 100%, part of the incident light passes through the structure element and reaches the viewpoint. This constitutes the transmissive property of the structure.
In volume rendering, both reflection and transmission are considered in order to create a rendition. In surface rendering, generally only the reflective property is considered, but when a fixed upper opacity that is less than 100% is assigned to the structures, transmission also needs to be considered for creating renditions.
Shading and Compositing : Shading is the process of determining the net intensity of light that is reflected toward the viewpoint from each structure element due to the combined effect of diffuse and specular properties. Compositing is the process of computing the net intensity of light that is emitted toward the viewpoint by each structure element because of its reflective and transmissive properties. Compositing hence includes the process of shading. Light may be white or colored.
Antialiasing : The effect of digitization of space in the form of cells introduces sampling artifacts which manifest themselves in renditions of the structures in various forms, in particular, in the form of discrete appearance of the individual cell boundaries. Antialiasing is a smoothing operation whose aim is to overcome these effects. It converts a rendition A into another rendition B. The pixel intensity in B represents an average of the intensities of a small square block (e.g., 22) of pixels in A. Since the blocks do not overlap, B is smaller in size than A. Usually the size of A is itself chosen to be n times the size of the desired picture B for a block size of nn, so that after the operation, B will have the desired size.
Registration : Suppose we are given an object assembly such as the head of a patient. The scenes may have been acquired at different times from an imaging device of the same modality (such as an MRI scanner) or from two different imaging devices of the same or different modality (such as an MRI and PET scanner). Suppose the scenes contain information about one object that has not changed shape and that is completely captured in the two scenes. Then we can "match" the two scenes by "matching" the two structures representing the same object, provided the structures can be identified accurately in the two scenes. To match the two structures we may need to translate, rotate, and scale one of them. Registration is the process of determining these geometric transformations given two scenes so that some common fixed information in the two scenes is matched accurately. Registration is required for combining complementary information from multiple sources (such as MR and PET images of a patient head) and for comparing information obtained longitudinally.
The scope of registration is more general than that indicated above when we consider this operation as applied to structure systems. Suppose we are given a structure system representing an assembly of rigid moving objects, such as a joint in action. For any given object, the structure system contains a sequence of structures that constitute the object position at different time instances during its motion. Therefore, by registering the successive structures in the sequence, we can determine the motion of the object. Thus, registration when applied to such a structure system gives motion description. Suppose the structure system represents a dynamic non-rigid object assembly such as the heart and its components. If we are given two such structure systems representing the same heart at two longitudinal time instances, we can apply registration to match the two systems if we can find a component (4D) object that has not changed its shape (as a 4D object). Such principles can be extended to structure systems containing both rigid and non-rigid objects coming from the same subject or from different subjects.
 User Manual
User Manual
 Library Ref. Manual
Library Ref. Manual
 Tutorial
Tutorial